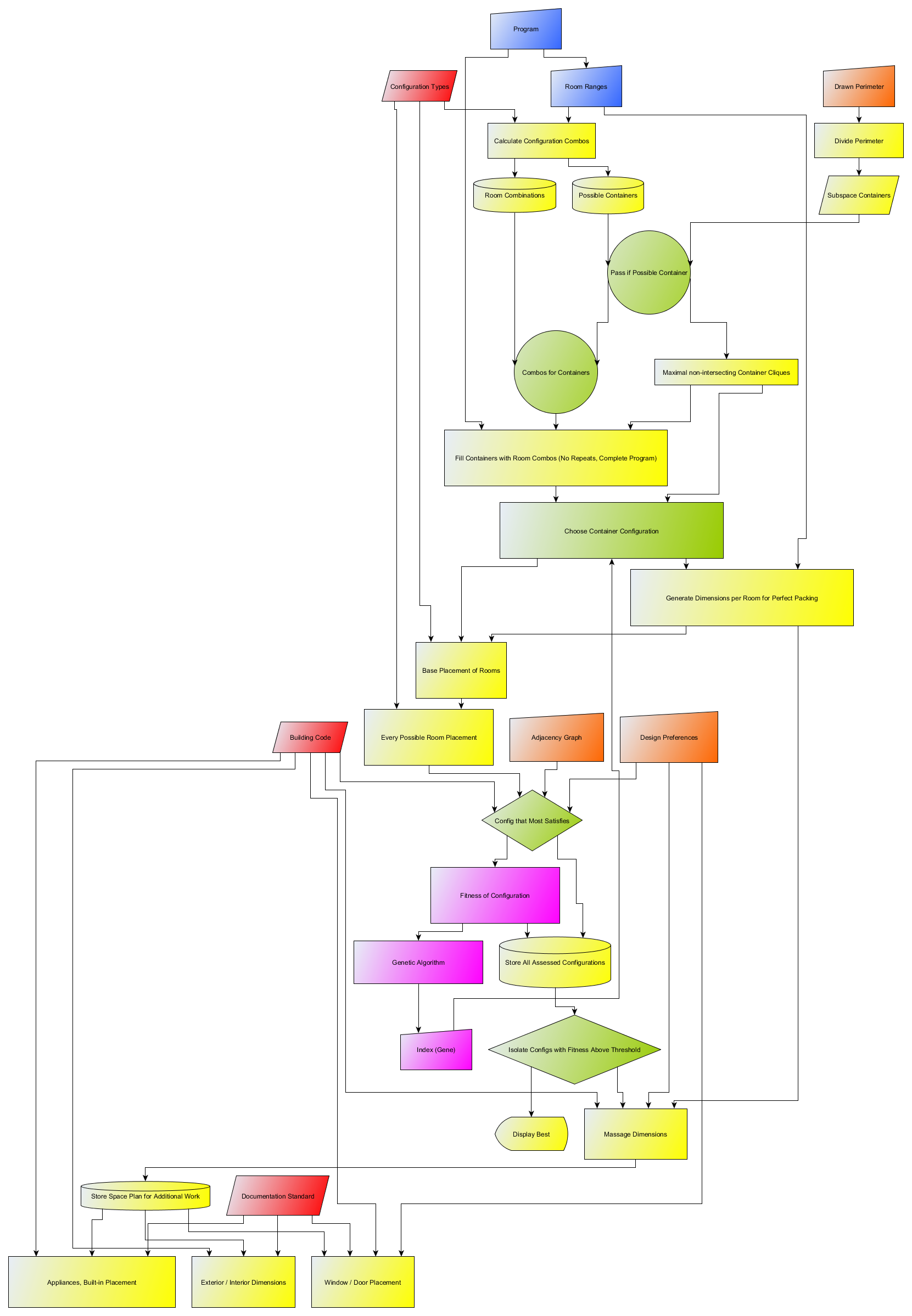
In the past few weeks I have done a lot of reshuffling of Archbot, with a near complete overhaul of the code. It has changed to be more elegant, efficient, and flexible, with the core concepts still intact. I am using Google’s Flux to help divide many of the tasks among a collection of GH files, separating processing that responds to fixed variables (building program) from processing that responds to design inputs (adjacency, perimeter, directional placement, etc.). This allows the algorithm to respond to real-time inputs with greater ease, a necessity I have mentioned before.

Here is a basic flowchart of the process for generating a space plan with Archbot:

The main goal is to give the designer strategic points to exercise freedom in the development of the design, while using power of computation to explore variety. I am trying to incorporate as many points of intervention as I can, so that the designer can pick and choose where they need to have greater control. For this initial development I have tried to set up a framework for design intervention, but if no input is desired forcing the algorithm to come up with everything after some initial inputs. As a self-trained coder, I have made many naive mistakes that break the process when certain tweaks are made. Through re-coding I have been able to make many aspects more dynamic. There are still parts that require that I hold its hand but I don’t see why most of them can’t be coded away eventually.

Below is an example of space plans being automatically generated. The inputs are a 14 space program and a 12 sided perimeter. The animation shows the algorithm dividing the perimeter, finding combinations of containers, packing those containers so as to place each space exactly once, and using a genetic algorithm to sift through the combos. The rooms are colored by how well the desired adjacencies are satisfied. The space plans are far from perfect, but the process is getting far more efficient. Next step is to get the adjacency weights and dimension massaging fine tuned.

This one shows the variety of placements for some combination of spaces within the containers. The pattern represents each way the packing can be arranged. Once again, the problem is a data structure / accounting issue that I just need to work through, but once I do I should be able to shortlist some ideal candidates based on by stated desirables. In the flow chart, this would be the part labeled “Config that Most Satisfies.” See below:

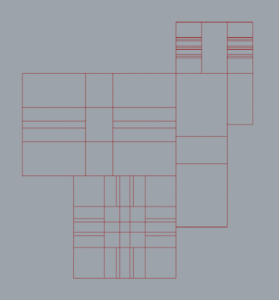The varieties shown above, however, are given a constant of specific containers. The container combination will determine the number of complete configurations that can form, which may or may not allow a configuration that would satisfy adjacency, flow, and orientation criteria. I am currently trying to understand which attributes of container combinations result in a greater probability of converging to a satisfying combination.

The containers above are natural chords, divided by extending the lines that create concave angles. Just to refresh:

Additional containers can be created by defining additional points within the space. These points can divide the space along the x-axis or y-axis. Choosing this point, or collection of points, herein CPoint(s), can create containers that are more suitable for satisfying all criteria.

To refresh: this method of creating containers within a space and then packing the containers with rooms is a way of aggregating the packing problem. When we enter space planning problem, we are given a set of rooms and a perimeter in which to fit them. If 14 rooms need to be placed, then the perimeter could be divided into 14 containers such that each room can fit perfectly in each container. This is quite difficult to accomplish, so the number of containers is typically less than the number of rooms, with a maximum packing for each container being 4. This makes the selection of the way the space is divided into containers very influential to how successful a resulting configuration can be.

It is too much to calculate everything at once, but by choosing a CPoint one at a time, I can assess how many Complete Programs (all rooms placed and the space completely filled), herein Csize, I would be able to explore. The higher the Csize for a given CPoint, the more options that can be explored, and for now I can only hope that this is a good thing. Once I have sufficient Csizes, I can begin to find correlations between the qualities of the containers created due to the selection of a CPoint, and a high Csize.

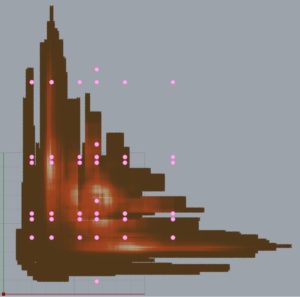
After running Galapagos for a few hours, I was able to generate this map of points.

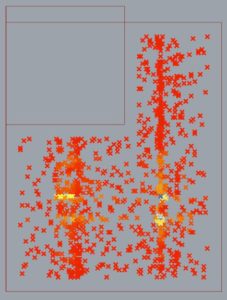
The red lines indicate the the geometries making up the perimeter geometry (the smaller rectangle is the placement of the garage). The points exist within the remaining space (with the garage subtracted) and offset the smallest possible dimension of a space (32″ for a closet). The color of each CPoint indicates the Csize and are displayed red->yellow->blue for small->large Csizes. As you can see, the areas that are non-red are spatially clustered, and I believe the reasons for this will be found in the collection of containers that they create. These containers have different potentials for packing rooms. It is intuitive that the clusters of higher Csizes do not exist on the fringes of the space.

Here is the CPoint with the highest Csize, and the division of the space:

Comparing these containers (pink) to the calculated containers gives this picture:

Despite being the CPoint with the highest Csize, there are only 27 out of the 40 cut containers that can be packed. Something about this combination of containers makes it more capable than all of the rest. Although I was inclined to think it was directly connected to the number of packings per container, there doesn’t seem to be a direct, or sole causation between them. It is likely a combination of causes including number of packings, the number of different rooms that can be packed into a container, the number of unique sets of rooms that can be packed into a container, etc. I hope to find a definitive metric that will give me a high confidence in choosing a CPoint that would generate a large number of Complete Programs, but I have my doubts. Perhaps it has more to do with the relation between the CPoint and the domain of all possible CPoints. I am not looking for absolute answers, which requires brute force, just high confidence. TBD.

After choosing a CPoint, the algorithm finds all Complete Programs and sifts through them to locate the highest satisfaction plan.

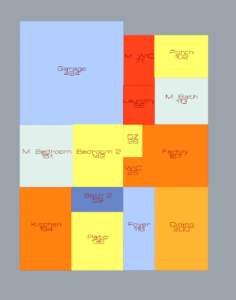
At this point I am wondering if I need to tweak the initial inputs for the rooms’ dimension ranges. The porches seem too big, and the Foyers are almost always long hallways. I want the Foyers to be like hallways if they need to be, but not all the time. Porches should be allowed to have a tight width like the Foyer so that it can be more of a stoop than and typical front porch. As always, more work to be done, but the flexibility is increasing.