As I develop the algorithm, I am often forced back to the beginning of a data stream to see if something more elegant could accomplish the same task. Working alone has given me flexibility to aggressively modify the algorithm in ways that would have faced more resistance in a team setting. I would love collaboration because personal eurekas can be harder to come by, but I have enjoyed the absence of a sunk cost that a team project might exhibit. In the spirit of starting over again, I’d like to cover some of the fundamental aspects to the algorithm.

I have started with 15 rooms and their respective size ranges (separated at 4″ masonry increments) for a single-family ranch house. Containers are rectangles that can perfectly pack some number of other rectangles. I have calculated all packed containers up to 4, and one packing of 5, and I have defined all desired adjacencies in a graph. From the set of containers, I want the algorithm to select combinations that would create complete cliques for the 15 rooms, while also allowing desired adjacency. This is optimizing what is geometrically possible by a metric of adjacency satisfaction.

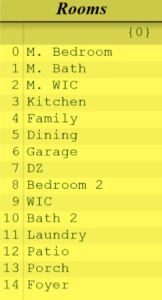
Aggregating the rooms to container combinations can simplify space planning of the whole building to fewer elements. Some adjacencies will fit nicely within a container, others between rooms will depend on the configuration of their containers. I could find a complete clique if I have a collection of 15 containers, each containing 1 room, or 1 container packed with 15 rooms, but the first is no different than just having 15 rooms, so the problem isn’t aggregated at all, and the latter is extremely difficult to process. The idea is to find a balance between these difficult scenarios, which is why containers packed with more (>1), but not too many rooms, is a happy medium. If considering containers that have up to 4 rooms packed, and the maximum number of containers is 6, the combinations are limited to 14 different collections of container lengths (max length 7 has 23 sets, max length 8 has 31 sets, max length 9 has 38 sets).

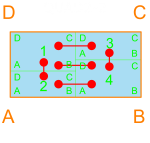
Below is the list of sets for a maximum of 6 containers. Each set is the collection of container sizes that could result in a complete graph. For example, the first set (1, 1, 1, 4, 4, 4) means that I can have three containers, each with 1 room, and three containers, each with 4 rooms, to possibly create a complete graph, since 1 + 1 + 1 + 4 + 4 + 4 = 15. Each set listed adds to 15. The difficult stipulation is that each room in the set must be different.

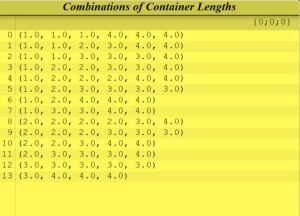
For the container set of (1, 1, 1, 4, 4, 4) I could have a complete graph with these containers, but also many others:

[Porch]
[Patio]
[Garage]
[M. Bedroom, M. Bath, M. WIC, Kitchen]
[Laundry, Bath2, DZ, WIC]
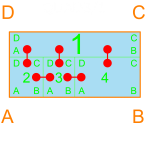
[Family, Dining, Foyer, Bedroom 2]

Depending on the design, certain sets can be more desirable. If it is desirable that the perimeter is a perfect rectangle, then packing all 15 rooms into one container would work. Since that is difficult, maybe packing just a few qualifying containers into the perimeter would work better. Take #13 from the list above as an example, with a rectangle as the perimeter. This would mean that a qualifying arrangement would involve a set of containers of lengths (3, 4, 4, 4), and these containers would fit within the rectangular perimeter like any of the Quad packings. As the perimeter becomes more complex, other container combinations may become more appropriate, depending on how that can be divided. Here are just a few examples of simple rectilinear polygons of 4, 6, and 8 sides:

The maximum clique problem is well known in math and computer science, and poses a difficult barrier to quickly exploring the variety that is possible. Having the guide above provides a shortcut to generating complete cliques. Through the adjacency graph and container combos, I can explore combinations that may have higher probability of generating satisfying plans. Though it is not necessary to pack all desired adjacencies within a container, it will be more desirable than not. Some container configurations are more suitable for satisfying certain adjacencies, therefore it is important to understand what value each container configuration has for adjacency.

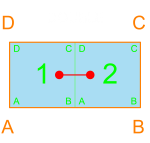
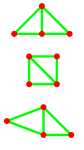
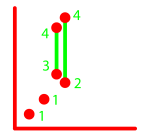
A Double is easy to define. Room 1 is adjacent to room 2, and vice versa.

The conditions to find this container combo are fairly simple (probably not a proper high-level description, but here goes):

Input: container dimensions, two candidate dimension ranges (i.e. room1, room2)
Output: Double (pairs of rooms that create a Double packing condition)
RangeY = YRange_room1 & YRange_room2
RangeX = [min(XRange_room1)+min(XRange_room2), max(XRange_room1)+max(XRange_room2)]
if AD_container in(YRange) && AB_container in(XRange):
    Double <= [room1, room2]

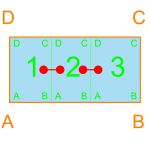
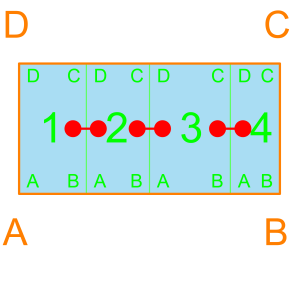
Triple0 is much the same, but with one more room stacked. As shown, room 2 is adjacent to room 1 and room 3, but rooms 1 and 3 are not adjacent. So if all three rooms must be adjacent to one another, this would not be a good configuration. With higher number containers that are stacked in such a way, the endpoints will have just one adjacency, whereas the middle points will all have two adjacent rooms.

 

The code is nearly the same between Triple0 and Double, just with one more room added.

Input: container dimensions, three candidate room dimension ranges (i.e. room1, room2, room3)
Output: Triple0 (three rooms that create a Triple0 packing condition)
RangeY = YRange_room1 & YRange_room2 & YRange_room3
RangeX = [min(XRange_room1)+min(XRange_room2)+min(XRange_room3), max(XRange_room1)+max(XRange_room2)+max(XRange_room3)]
if AD_container in(YRange) && AB_container in(XRange):
    Triple0 <= [room1, room2, room3]

 

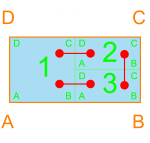
Triple1 can provide adjacency between all three members of the container, providing something different than Triple0. The code for Triple1 is just an extension of Double, since rooms 2 and 3 form a Double, which then creates a Double (as a container) with room 1.

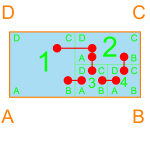
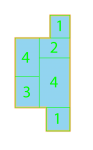
Quad0 is probably less common in a single-family residential setting, but more common in institutional or commercial settings. Rooms 2 and 3 each have two adjacent rooms, but 1 and 4, just one. If rooms 1 and 4 here (and 1 and 3 in Triple0), have more than one adjacency, as they likely will, it will have to be through the configuration of the containers.

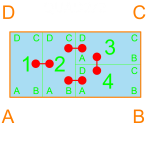
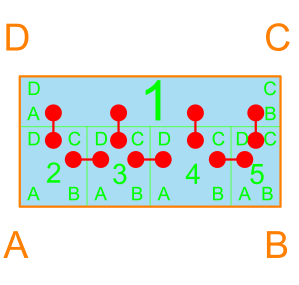
In terms of adjacency, Quad-S, Quad2-2, Quad3/1 are all the same, with two rooms having two adjacent rooms and the other two rooms having three adjacent rooms. The difference in their configuration will be appropriate based on proportion, flow, and outside adjacency.

Quad2-2 depends on the relative sizes of the Doubles. The larger room in the double gets the advantage of three adjacencies, the smaller – two adjacencies. Just considering adjacency isn’t the only story. Although these three have the same adjacency graphs, they have different edge costs, and is a factor in their viability. The adjacency between 1 and 4 in Quad2-2 as shown would be a good candidate for rooms that need a simple access point (a door).

Quad2/2 has a variety. Room 1 is only adjacent to room 2, but room 2 has adjacencies with all other rooms. Rooms 3 and 4 each have 2 adjacencies.

 

Quad4/1 is more appropriate for institutional or commercial. If the proportions are similar to as shown, room 1 is best suited for storage, mechanical, or circulation, but could be lobby / ballroom type space if the AD dimension was greater. At this point, though, I would rather the algorithm naturally place or ignore such a configuration due to its inherent ability to satisfy adjacency (or not) rather than removing it from consideration.

I need to become more familiar with dictionaries so that less code is needed and the code can scale automatically. For stacking configurations, however, it is much simpler to generate combinations through geometric computation. For each room there is a predefined XRange and YRange. I know that a room will not have a dimension of zero, nor infinity. There may be some desirable dimension, but through SD and DD phases, these dimensions may drift from this number (as well as perfect rectangular shape, obviously, but that for later). Due to this shift, I find it reasonable to assign ranges to the rooms.
One element from the XRange set can be paired with any member of the YRange set, and vice versa, heeding the 4″ increment rule. A pair will create the rectangle for that space, but there are multiple possible rectangles that can be created. Create all of these rectangles, and align the bottom left corner (A) of each with the origin point at (0,0,0).

Now, each rectangle has the same position for A. Each B point is on the x-axis at y=0. Each D point is on the y-axis at x=0. Really, the only information needed is the position of the C point since that will determine the positions of points B and D.

Now, with all of the C points graphed, they will create a rectangular grid of points, which essentially means that the many different options for the sizes of room (48 shown above) can be defined simply by a single rectangle positioned somewhere in the cartesian plane.

These rectangles are essentially the probability spaces for these rooms. Now, imagine arrays of XZ and YZ planes intersecting these rectangles. If two rooms intersect the same XZ plane, that would mean that they can have the same Y-dimension, and can therefore create a Double (as in the Double configuration shown above). The possible X-dimension for that double would be the sum of their XRanges. For example, if room1 has an XRange of [48,84] and room2 has an XRange of [100,140], then the XRange for the container would be:

XRange_Double = [min(XRange_room1)+min(XRange_room2),max(XRange_room1)+max(XRange_room2)]
XRange_Double = [48 + 100, 84 + 140]
XRange_Double = [148, 224]

For a stack of n rooms (Double, Triple0, Quad0, etc), the range would be:

XRange_Double = [min(XRange_room1)+...+min(XRange_room_n),max(XRange_room1)+...+max(XRange_room_n)]

Additional Plane / Rectangle intersections are quick ways to group the rooms, and dealing with 2D ranges rather than large sets of individual possibilities cuts down tremendously on processing time. I am not entirely familiar with the heuristics of geometric computation, but understand that it is a clever way of dividing up the space into more relevant quadrants to perform certain operations, such as intersections. Although I could incorporate such methods into code, I find it simpler for the task at hand to make use of this very useful way of performing operations. After all container combinations are calculated, a collection of ranges that represent the container sizes can be generated, similar to the ranges for the individual rooms:

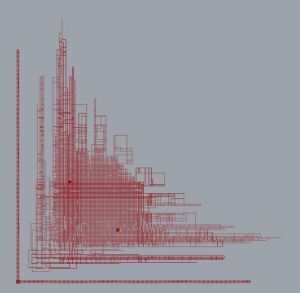
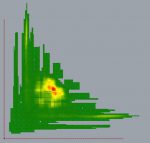
The geometry displayed consists of 7,752 different pieces of geometry corresponding to unique container configurations; from rectangles, to lines, to points. A line means that changes in scale can only happen along one axis, and points mean that there is just a single size for that container combination. When this geometry is broken down to the individual containers (points) that it represents, it is possible to get an idea of what container sizes are most common across all of the types of configurations calculated (Match, Double, Triple0, Triple1, Quad0, Quad-S, Quad3/1, Quad2/2, Quad2-2, and Quint4/1).

The global maximum occurs at the perfect square with sides 24′-8″ with a total of 796 instances. There are also many high count containers surrounding this container along the line y=x of perfect squares, nearly square rectangles, and containers with a dimension of 12′ maxing out at dimensions of 12′ x 52′ (which are shown as the yellow regions further along the axes). This data is a direct result of the number of rooms and their respective ranges, therefore is only applicable to the 15 rooms and the ranges that I have assigned them. It took over 20 minutes to process this data into what is shown here, since the list had over 680,000 containers, with over 12,000 unique sizes. The good thing is that is just needs to be generated once, and subsequent analysis can yield smaller, more manageable data sets. Analyzing this can give an idea for possible perimeter and offset dimensions that would possibly lead to the greatest variety of floor plans. This data does not directly represent the number of possible placements for complete graphs, but there may be a correlation. This will require further investigation.

The data shown is the design space for the number of rooms, their rectangular shapes, and their chosen ranges. However, this shows the possibilities before any design decision is made for a combination. Once any decision is made regarding a room size, or a range for a combination of rooms, the possibilities are cut down to a subset of what is shown. With each subsequent decision, the design space becomes more limiting. Despite this, there are still millions of possible combinations that can be assembled. The trick, as I see it, is to find strategic ways of limiting the design space and then making a decision.

For example, if I isolate combinations that must satisfy container lengths of sum(1, 1, 2, 3, 4, 4)=15 and generate a heuristic list of possible combinations, I get down to a list of 5315 unique combinations of containers (and each container, its different combination of rooms). Although 5315 is a large number, it gets much larger (over 9mil) when considering the possible container sizes ranges (Triple0, Triple1 for 3 – Quad0, Quad-S, etc. for 4) and larger still for each individual container size. Below shows different possible combinations of sizes for the containers. The (1,1) containers are red and pink, (2) is green, (3) is yellow, (4,4) are blue and light blue, thus you will notice that red and pink are smaller, and the blues are usually the largest (furthest from origin). There are multiple range geometries for some of the colors due to the number of different configurations per room combination. Matches and Doubles will have fewer possible versus Triples and Quads (e.g. a Quad packing with rooms (0, 1, 2, 3) could make a Quad0, Quad-S, etc. of many different sizes).

Relations between container sizes might be favorable for certain types of floor plans allowing for the creation of Doubles, Triples, & Quadruples with the containers. The example below shows a configuration where 4 of the containers actually form a Quad2-2, and graphing their container sizes yields two disconnected points (1,1) and a set of vertical, parallel lines. In this particular case, the sum of the heights of (3,4) and (2,4) can be equal, making them compatible for this particular configuration where (2, 3, 4, 4) create a Quad2-2. If, instead, it had a Quad2/2 arrangement, the lines for (3,4) and (2,4) would be in perpendicular directions. The selected sizes of the containers could be anything, but sizes and relationships offer different opportunities.

Relationships between points in the XY plane tell stories. It is reductive, much like how facial recognition software analyzes a face based on the location of certain facial features. The pattern of a building will have far more feature points than simple facial recognition systems, but the features of the “face” should hopefully be simpler to recognize. This leads to the question of questions – Computer, computer, plugged into the wall, which floor plan is the most optimal of all?